Demonstre que a soma dos quadrados das diagonais de um paralelogramo é igual ao dobro da soma dos quadrados dos lados.

Fala, galera! Confusos em como demonstrar essa propriedade? Não se preocupe que a gente Responde Aí para vocês.

Todo paralelogramo tem lados opostos iguais. Isso quer dizer que só precisamos de dois vetores não paralelos para caracterizar um paralelogramo. Vamos dizer que esses vetores sejam e . Não é tão difícil ver que e são as diagonais desse paralelogramo (veja a figura abaixo)

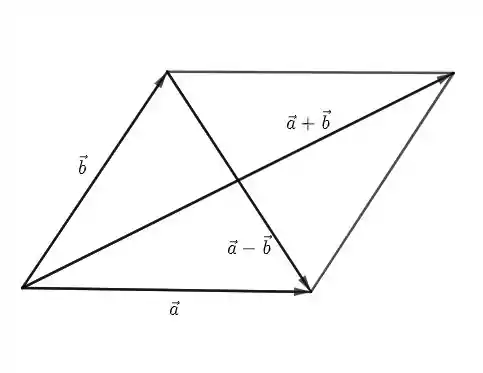
Agora vamos calcular os quadrados das diagonais:

Agora, só precisamos somar:

Taí o resultado que o livro queria: a soma dos quadrados das diagonais de um paralelogramo é igual ao dobro da soma dos quadrados dos lados.