Descreva o conjunto de pontos que satisfazem a condição indicada.
- e
Passo 1
Olááá, tudo bem??
Nessa questão vamos trabalhar com inequação e antes de pôr as contas na ponta do lápis, vamos fazer uma rápida revisão de suas propriedades.
Diferentemente de uma equação, a inequação do 1º grau expressa uma desigualdade na variável que pode ser reduzida em uma das formas
Em que e . Esses sinais servem para comparar. Para resolver uma inequação do 1º grau, deve-se determinar um conjunto com todos os valores para a variável de forma que a sentença se torne verdadeira.
Passo 2
Agora que compreendemos as propriedades no Passo 1, vamos começar a resolução dos itens.
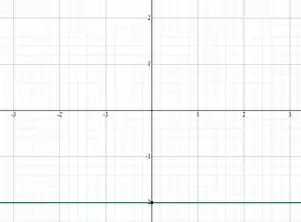
- A equação dada é uma reta paralela ao eixo que intercepta o eixo n ponto , logo todos os valores de em satisfazem a condição, como mostra a figura abaixo
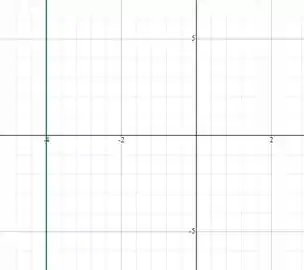
- A equação dada é uma reta paralela ao eixo que intercepta o eixo n ponto , logo todos os valores de em satisfazem a condição, como mostra a figura abaixo
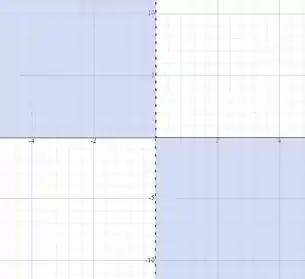
- A equação dada apresenta uma restrição de que a divisão . Lembre-se que para que a divisão seja negativa ambos os termos devem ter sinais opostos, ou seja, e , logo todos os valores que estão no 2° e 4° quadrante, satisfazem a condição, como mostra a figura abaixo
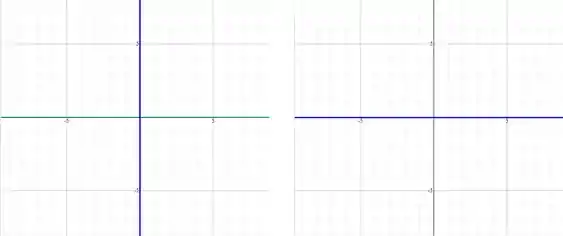
- A equação dada apresenta uma restrição de que o produto . Lembre-se que para que o produto seja igual a um dos termos deve ser igual a , ou seja, ou , logo todos os valores que estão ou no eixo ou no eixo satisfazem a condição, como mostram as figuras abaixo
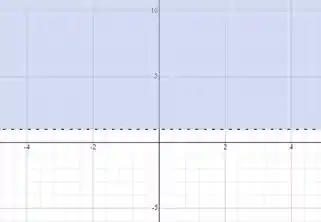
- A equação dada apresenta uma restrição de , logo todos os valores acima do eixo no ponto satisfazem a condição, como mostra a figura abaixo
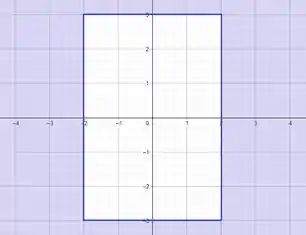
- A equação dada apresenta duas restrições de e , que correspondem, respectivamente, aos intervalos , , e , logo todos os valores contidos nas bordas e fora no retângulo formado pela intercepção desses intervalos satisfazem a condição, como mostra a figura abaixo
Passo 3
Passo 4
Passo 5
Passo 6
Passo 7
Até a próxima! =]