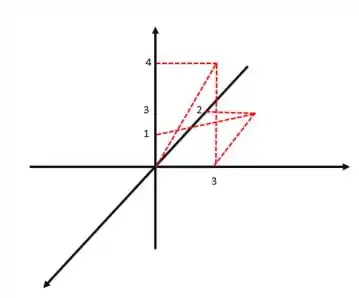
Descreva e represente graficamente os seguintes conjuntos de pontos:
Passo 1
Falaaaaa rapaziada tudo blz?
Nesta questão ele pede para descrever graficamente os conjuntos dos pontos
Nesta questão o que precisamos determinar com base nesses dados quais os eixos e vértices da função.
Passo 2
No ponto A dado que
Note que ele diz que tendo só como eixo a reta z, a partir daí podemos dizer que está equação tem eixo z
No ponto B dado que
Mesma coisa que a reta anterior só que nessa temos os pontos a partir daí ficamos com
paralelo ao eixo z
No ponto C dado que
Nessa aqui só temos o ponto z com isso
sendo com isso,
Plano paralelo ao eixo
Passo 3
No plano D tendo
Nessa todos os pontos vão ser zero pois o e os outros são dados como igual a zero
Ficando o plano
E o plano E tendo
E nessa ela vai ser diferente pela função dada temos uma circunferência tendo raio 1
Com isso sendo um cilindro circular reto de raio 1 ficando,
O eixo coincidindo com o eixo z
Resposta
Equação tem eixo z
paralelo ao eixo z
Plano paralelo ao eixo
Ficando o plano
O eixo coincidindo com o eixo z