Determine uma bse e a dimensão dos seguinte subespaços de .

Passo 1
- O sistema que representa o hiperplano (x,y,z,w) Є já está escalonado, portanto, a equação dada tem 4 variáveis do plano e 3 variáveis livres, ou seja, as representadas na equação, logo a dimensão é 3. Se escrevermos a equação em função de x como dependente e y,z,w como livres, teremos:
- O primeiro passo é escrever o sistema como uma matriz e escalonar da seguinte forma:
- O sistema solução já está escalonado, então basta fazermos as análise, das seguintes equações:
- A ideia para resolver a letra D é fazer o processo inverso do que nós estávamos fazendo, logo, o primeiro passo é reescrever a equação parametrizada:
Portanto: , logo a base pode ser escrita por:
Passo 2
Ou seja, temos:
São duas equações das quatro variáveis (x,y,z,w), portanto, a dimensão é 2. Para obtermos as base, vamos associar à equação x e z como variáveis dependentes e y e z como livres, assim:
Portanto: , logo a base pode ser escrita por:
Passo 3
São duas equações das quatro variáveis (x,y,z,w), portanto, a dimensão é 2. Para obtermos as base, vamos associar à equação y e w como variáveis dependentes e x e z como livres, assim:
Portanto: , logo a base pode ser escrita por:
Passo 4
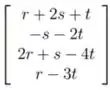
Esses termos encontrados vão ser escritos em forma matricial e depois faremos o escalonamento, assim:
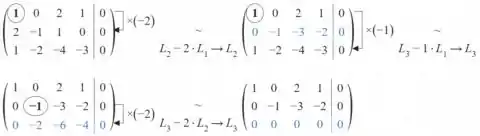
Portanto, a contagem das linhas não-nulas da matriz representa a dimensão do espaço que é 2, além disso as linhas também representam a base, logo,
Resposta
- 3;
- 2;
- 2;
- 2;