Determine como deve variar o módulo e o sentido de (isto é, por quais constantes se deve multiplicar ) para que a resultante destas forças seja , sendo . Veja a figura 2.17b
Passo 1
Falaaaaa rapaziada tudo blz?
Nesta questão temos que determinar como deve variar o modulo de sentido dado que,
,
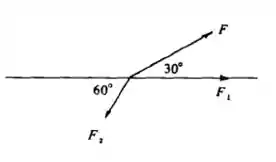
Precisamos entender que nesta questão vamos precisar decompor todas as forças que não estão na horizontal.
Passo 2
A partir daí vamos ter que,
Equacionando o problema temos,
Com isso, vamos ter que
Resposta