a) Determine a distância de uma diagonal de um cubo a cada uma de suas arestas.
b) Unindo-se o centro de uma face de um cubo com os vértices da face oposta, obtém-se uma pirâmide de base quadrada. Determine os ângulos entre os planos das faces da pirâmide.
Passo 1
Falaaaaa rapaziada tudo blz?
Nesta questão ele pede para determinarmos os itens mencionados em,
a) Determine a distância de uma diagonal de um cubo a cada uma de suas arestas.
b) Unindo-se o centro de uma face de um cubo com os vértices da face oposta, obtém-se uma pirâmide de base quadrada. Determine os ângulos entre os planos das faces da pirâmide.

Passo 2
Na letra (a) Para considerarmos a distância de uma diagonal de um cubo a cada uma de suas arestas temos que,
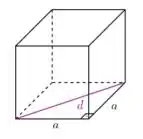
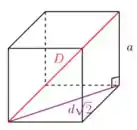
ou zero
Passo 3
Na letra (b) para determinarmos a fórmula para o ângulo que fica,
Ficando,
ou

Resposta
a) ou zero
b) ou