a) Determine a equação da reta que melhor ajusta os pontos e .
b) Esboce um gráfico ilustrando o item anterior.
c) Use sua resposta ao item (a) para determinar a projeção ortogonal de sobre .
Passo 1
Beleza, pessoal? Vamos fazer mais um!!!
a) O exercício consiste em encontrar o vetor que satisfaz o sistema abaixo:
A matriz estendida desse sistema é dada por:
Escalonando-a, obtemos o seguinte:
Portanto, o sistema possui uma equação degenerada, donde concluímos que ele não possui solução. Sendo assim, devemos encontrar uma solução de mínimos quadrados , ou seja, um vetor que satisfaz o sistema abaixo:
A matriz estendida desse sistema é dada por:
Escalonando-a, obtemos o seguinte:
O que nos oferece a solução e . Logo, a reta é a que mais ajusta os pontos e .
Passo 2
b)
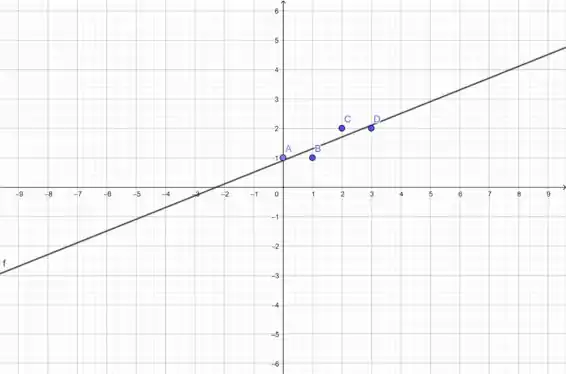
Passo 3
c) Temos que a projeção ortogonal de em é dada por:
Resposta
a) .
b) Imagem acima.
c) .