Determine os focos, os vértices e esboce as hipérboles cujas equações são:
Passo 1
Falaaa, blz?? Vamos começar pegando a equação dessa hipérbole e colocando do jeito mais comum:
Vamos dividir toda equação por
Multiplicando ambos lados por -1:
Passo 2
Agora fica bem mais fácil achar o que precisamos, uma vez que sabemos que se trata de uma hipérbole com os focos sobre o eixo y, ou seja, uma hipérbole vertical com centro na origem.
Sabemos pela equação que:
Pela relação
Como os focos são do tipo
Passo 3
Escrever 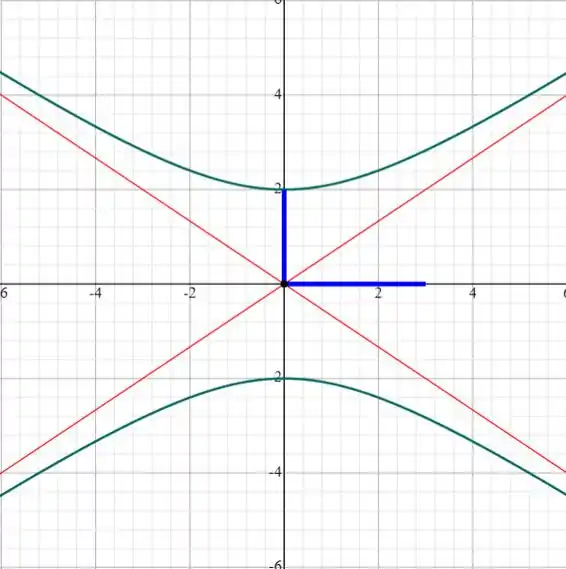 aqui
aqui