Determine se formar um subespaço vetorial do subconjunto de todos os vetores:
a) com exceção daqueles paralelos a uma reta dada;
b) cujas coordenadas são maiores ou iguais a zero;
Passo 1
E aí, pessoal, tudo certo? Bora resolver mais esse!!!
Antes de tudo, vamos lembrar como é caracterizado um subespaço vetorial. Seja um espaço vetorial e , temos que é um subespaço vetorial se:
1- ;
2- é fechado para soma vetorial, ou seja, se então ;
3- é fechado para multiplicação por escalar, ou seja, se e então ;
Sabendo disso, vamos aos itens!!!
Passo 2
a) Podemos ver pela imagem abaixo, que somando dois vetores não paralelos a reta, podemos obter um vetor paralelo a reta, ou seja, o subconjunto não satisfaz a segunda condição para ser um subespaço vetorial, de modo que podemos concluir imediatamente que ele não é um subespaço vetorial de .
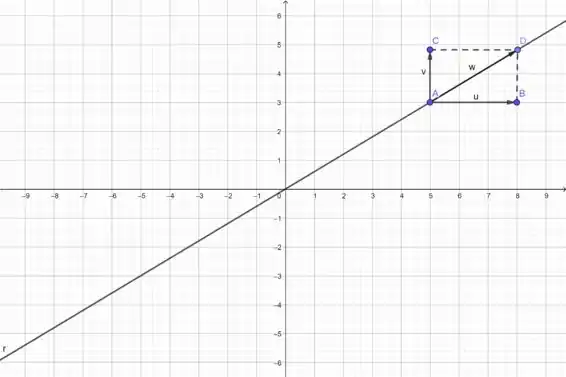
b) Seja com e um vetor do nosso subconjunto. Agora, seja um real com , temos que com e , ou seja, não pertence ao nosso subconjunto. Sendo assim, o subconjunto não satisfaz a terceira condição para ser um subespaço vetorial, de modo que podemos concluir imediatamente que ele não é um subespaço vetorial de .
Resposta
a) Não é subespaço vetorial de .
b) Não é subespaço vetorial de .