Determine matrizes X e Y de modo que possua autovalores 2 e -3 com autovetores associados, respectivamente,
![]()
Passo 1
Para resolvermos essa questão de uma forma bem facinha, basta lembrar as condições que tornam uma matriz diagonalizável se existe P invertível tal que com A diagonal. Se nós prestarmos atenção, essa função é bem similar a , portanto, pode-se dizer que as colunas de P são autovetores na diagonal de y. Para isso, X deve ser:
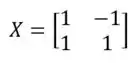
Passo 2
E matriz diagonal Y representa os autovetores fornecido no comando, sendo cada coluna um, portanto:
![]()
Resposta
![]()