Determine o ponto da elipse mais próximo da reta 2x-3y+25=0
Passo 1
Vamos começar essa questão fazendo o seguinte desenho:
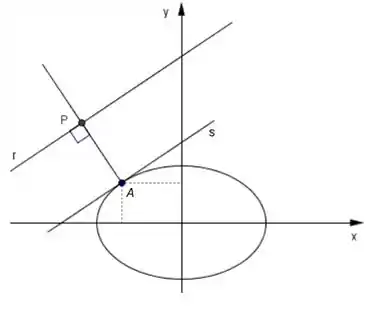
Perceba que o ponto que procuramos é o ponto A, pertencente à reta tangente s
Da equação da elipse temos:
Iremos ignorar o caso negativo pois no nosso ponto A, temos que o y é positivo
Derivando essa equação achamos:
Passo 2
Pela equação da reta r:
Logo o coeficiente angular da reta r é , como a reta s é paralela com a reta r, temos que sua inclinação é também, logo:
Daqui tiramos que
Passo 3
Ou seja, como temos o valor de x podemos substituir na equação inicial de y:
Então A = (-3,2)
Resposta
(-3,2)