Determine se é rotação, reflexão ou projeção ortogonal e eixo de rotação ou plano de reflexão/projeção de:
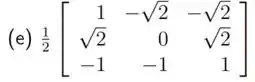
Passo 1
Opa, vamos resolver mais essa questão?
O primeiro passo é obter a matriz resultado da multiplicação, assim temos:
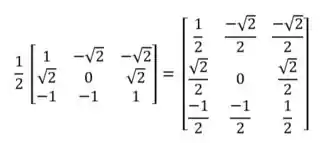
Passo 2
O segundo passo é pegar a matriz obtida e obter os autovalores, a gente vai fazer isso de uma forma bem fácil, saca só! Vamos observar a diagonal da esquerda para a direita e subtrair λ, dessa forma:
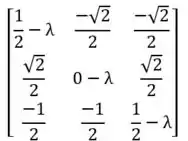
Aplicando o processo de achar o determinante, temos a seguinte equação:
Nessa equação nós percebemos uma informação interessante, a presença de valores imaginários, mas o que isso significa? Bom, se desenvolvermos a equação teríamos também valares complexos não-reais, portanto, essa matriz representa um movimento de rotação.
Resposta
e) rotação