Determine o valor exato da expressão, quando for definido.
Passo 1
Olááá, tudo bem??
Nessa questão vamos trabalhar com funções trigonométricas inversas e antes de pôr as contas na ponta do lápis, vamos fazer uma rápida revisão de suas propriedades e relembrar a tabela de ângulos notáveis.
— 1° Propriedade (Definição 8.1 e 8.2)
A função inversa do seno, denotada por “”, define-se como
Para e, . Em outras palavras,
— 2° Propriedade (Definição 8.3 e 8.4)
A função inversa do cosseno, denotada por “”, define-se como
Para e, . Em outras palavras,
— 3° Propriedade (Definição 8.5 e 8.6)
A função inversa da tangente, ou função arco tangente, denotada por “”, define-se como
Para todo e . Em outras palavras,
— 4° Propriedade (Definição 8.7)
A função arco secante denotada por “” (ou “”), define-se como
Para todo e em ou em .
Observe que estas funções estão limitadas a diferentes intervalos, logo valores que não pertencem a estes intervalos respeitam as propriedades de arcos côngruos e a paridade das funções.
Em seguida, temos a tabela de ângulos notáveis como conhecemos no ensino médio.
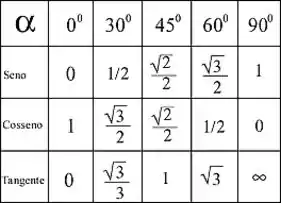
A imagem abaixo mostra os valores dos ângulos da tabela correspondentes nos demais quadrantes.
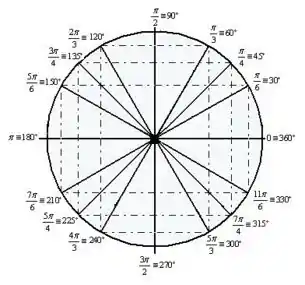
Passo 2
Compreendendo as propriedades das funções trigonométricas inversas, vamos resolver a questão.
- Temos que,
- Temos que,
- Temos que,
Por definição,
Sabendo que
Já temos que o valor de . Para encontrar o valor de , vamos utilizar a identidade trigonométrica
Dessa forma,
Logo,
Passo 3
Vamos primeiro analisar a função de dentro
Assim,
O domínio de é limitado ao 1° e ao 4° quadrantes porque . Como um dos valores é negativo, o triângulo deve estar no 4° quadrante, como mostra a figura abaixo.
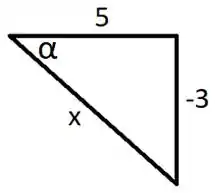
Com isso, para encontrar o valor de temos que calcular a hipotenusa (pelo teorema de Pitágoras) e dividir pelo lado adjacente, isto é,
Logo,
Só falta a resolução de mais um item, vamos lá!!
Passo 4
Sabemos que
Para o valor de . O domínio de é limitado ao 1° e ao 2° quadrantes porque . Como um dos valores é negativo, o triângulo deve estar no 2° quadrante, como mostra a figura abaixo.
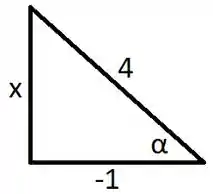
Com isso, para encontrar o valor de (lê-se: cossecante), temos que dividir o lado oposto (calcular pelo teorema de Pitágoras) pela hipotenusa, isto é,
Logo,
Até a próxima =]