Determine o vértice, o foco e a diretriz da parábola. Esboce o gráfico, exibindo o foco e a diretriz.
Passo 1
Eaew, tudo certinho contigo? Bora fazer mais um exercício de geometria analítica?
Para resolver este problema vamos utilizar o formato mais geral de uma parábola dado por:
ou
em que
Temos que e são as coordenadas do vértice e que é a distância do vértice ao foco, que é igual à distância do vértice à diretriz da parábola. Com isso temos tudo que precisamos para resolver a questão, belezinha?
Passo 2
Comparando nosso enunciado com a equação 2, temos que , e que . portanto . Com essa informação, podemos agora buscar mais informações sobre nosso vértice. O vértice é o ponto onde temos uma tangente horizontal, ou seja
Portanto, temos que nosso vértice está no ponto . Temos também que o foco está à uma distância do vértice, ou seja, , e por último, a diretriz é a reta horizontal estabelecida por . O esboço do gráfico é tal que:
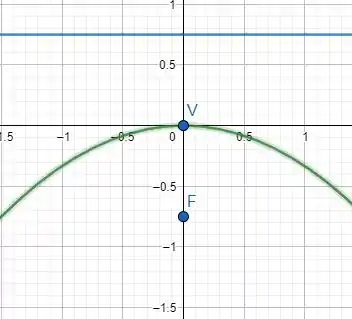
A questão é isso! Bora para a próxima?
Resposta
Ao longo do passo 2.