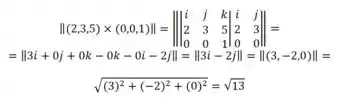Determine:
a) a distância do ponto à reta
b) a distância do ponto a cada um dos eixos do sistema de coordenadas.
Passo 1
Vamos começar relembrando como se calcula a distância de ponto à reta:
Temos que conhecer um vetor diretor da reta, um ponto qualquer que pertença à reta e o nosso ponto (o ponto cuja distância iremos calcular).
Assim, a distância será
Passo 2
a)Conhecendo o ponto e a equação da reta :
O vetor diretor pode ser obtido pelos termos que acompanham o parâmetro . Assim, .
Para , temos que . Então, podemos chamar de ponto o ponto já que vimos que ele pertence à reta.
Então
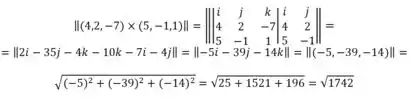
Assim, encontramos a distância .
Passo 3
b) Tendo o ponto como ponto e equação dos eixos de coordenadas sendo :
Eixo x:
Então o vetor diretor será e podemos considerar o ponto .
Então
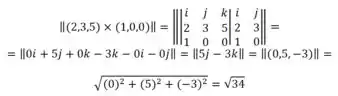
Eixo y:
Então o vetor diretor será e podemos considerar o ponto .
Então

Eixo z:
Então o vetor diretor será e podemos considerar o ponto .
Então