Diagonalizabilidade e invertibilidade são conceitos distintos. Para confirmar esta afirmação, construa uma matriz 2x2 que é:
- Diagonalizável mas não é invertível;
- Invertível mas não é diagonalizável
Passo 1
A ideia é resolver essa questão só com a lógica, olha só: para que uma matriz seja invertível seu determinante deve ser diferente de zero, em comparação, para que uma matriz seja diagonalizável se existe uma matriz inversível P e uma matriz diagonal D tal que .
Passo 2
a) Então, para montarmos uma matriz 2x2 que satisfaça a condição de ser diagonalizável, mas não invertível, devemos zerar o determinante, o que pode ser facilmente feito colocando 0 nas duas entradas de uma das linhas da matriz, dessa forma:
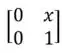
Como a informação que importa é que as diagonais sejam zeradas, pode ser qualquer número real. Ah beleza, já entendemos que essa matriz não é invertível, mas como saber se é diagonalizável? Fácil fácil, vamos assumir qualquer valor real para x, por exemplo se x=2, e descobrir se a matriz possui autovalores, dessa forma:
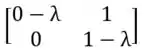
Desenvolvendo a matriz temos . Portanto os autovalores são , logo, a matriz é diagonalizável, mas não é invertível!!!
Passo 3
b) Continuando, para montar uma matriz 2x2 que seja invertível, mas não diagonalizável, temos que garantir que o determinante seja diferente de zero, ou seja, uma das diagonais deve ter todos os termos número reais, podemos colocar 1, por exemplo: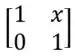
Sobre a outra diagonal tem uma informação importante, para que a matriz seja diagonalizável, devemos ter o número de autovalor igual à dimensão da matriz, então nós temos duas possíveis situações:
1) x=0:
![]()
Nesse caso, nós teríamos 1 único autovalor, , e a dimensão da matriz também seria 1, logo a matriz seria diagonalizável;
2) x≠0, por exemplo se x=2:
![]()
Nesse caso, nós teríamos 1 único autovalor, , porém a dimensão da matriz seria 2, logo a matriz seria não é diagonalizável.
Portanto, a matriz
![]()
é invertível, mas não é diagonalizável!
Resposta
![]()