Diagonalize, sem fazer contas

Passo 1
Uma boa forma de resolver essa questão é usar a lógica e perceber que se o determinante da matriz é nulo, um dos autovalores é zerado, além disso, todas as entradas são 5, então um autovalor é somar 5+5+5=15 que também é um autovalor. Ah mas ficou difícil de visualizar? Tranquilo a gente pode desenvolver a matriz para encontrar os autovalores, saca só:
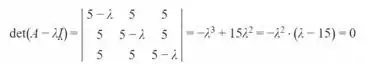
Portanto
Além disso, a matriz diagonal D é composta pelos autovalores, assim:
![]()
Passo 2
Para determinarmos os autovetores, basta substituir os autovalores da matriz obtida e resolver por eliminação de Gauss
- Se
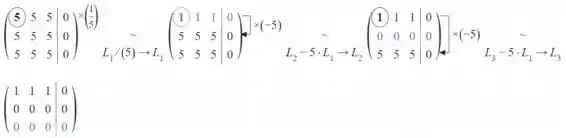
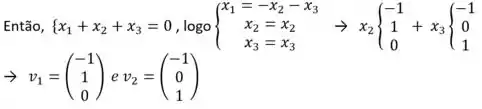
- Se vamos repetir o mesmo processo:
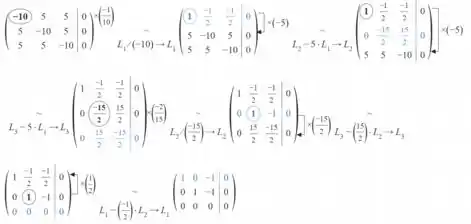
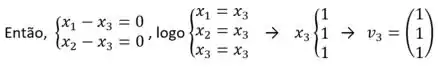
Passo 3
Portanto, os autovetores correspondente aos autovetores, sendo cada um corresponde à uma coluna:
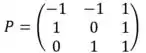
Resposta
![]()