(a) o eixo em , então é a reta _____ ;
(b) a reta em , então é a reta _______ ;
(c) o eixo em , então é o _________ (plano; eixo) __________;
(d) o plano em , então é o ________ (plano; eixo) _______
Passo 1
Diz aí galera! Tudo bem com vocês?
Pessoal para determinar as afirmações acima, fica mais fácil interpretar através dos gráficos que foram dispostos em cada item da questão: ;
Percebam que deixei esses gráficos na cor verde para
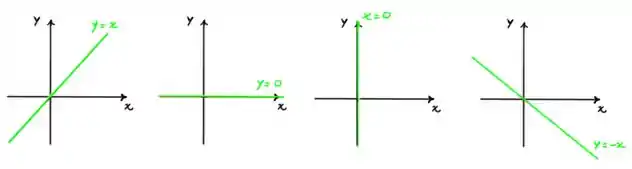 figura 1
figura 1
não esqueçam que devemos determinar que se trata do conjunto de vetores que são perpendiculares ao que nos foi dado, blz!
Agora para verificar os itens no vamos utilizar o gráfico abaixo
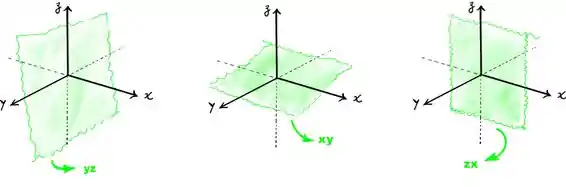
Simbora que vai dar certo
Passo 2
Para o item (a) devemos determinar qual item é perpendicular ao eixo vou deixar representado por uma reta vermelha.
Da figura 1 a única apresenta uma reta perpendicular ao eixo é o
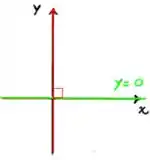
Passo 3
O item (b) vamos determinar qual é perpendicular ao gráfico (vou deixar representado por uma reta vermelha), para isso a única das opções disponível é , conforme a figura 1
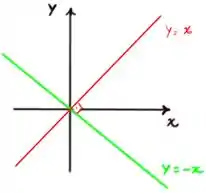
Passo 4
O item (c) devemos determinar no , se o conjunto é o _________ (plano; eixo) que seja perpendicular ao eixo (vou representar pela reta vermelha) pela representação do gráfico abaixo podemos terminar que todo o conjunto que é perpendicular trata-se de um PLANO, que por ventura é o plano xz
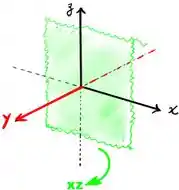
Passo 5
Estamos chegando no finalzim, para o item (d) basta verificar a perpendicularidade para o plano (representado pela região vermelha na figura abaixo)
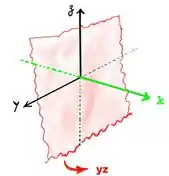
Olha só a reta verde galera que podemos perceber que trata-se de um EIXO e que é represente pelo
Resposta
(a).
(b).
(c). plano .... xz
(d). eixo ... x