4. Esboce os gráficos das elipses marcando os focos:
Passo 1
Galerinha, nessa questão não tem muito segredo. Todas as elipses dessa questão estão centradas na origem, então as coisas ficam mais simples. Só precisamos descobrir as extremidades e os focos. Para descobrir as extremidades, fazemos ou e resolvemos a equação. Para descobrir os focos, usamos a distância focal. Bora lá?
- O eixo maior é , o menor é e é dado por
- Vamos dividir a equação por
- Observando a elipse , dá pra gente notar que . Então, os focos estão no eixo . Além disso,
Como o eixo maior está em , então a coordenada dos focos é . Assim,
Fazendo , ficamos com
Fazendo , ficamos com
Agora que temos os focos e as extremidades dos eixos, podemos desenhar a elipse.
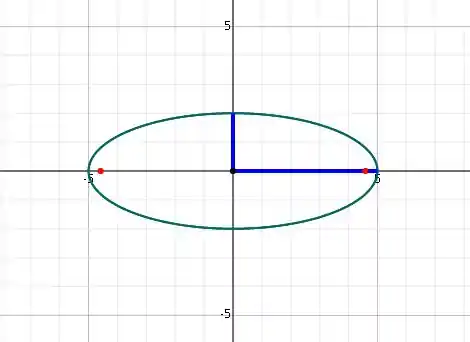
Passo 2
Assim, o eixo maior está em temos , e
Então, os focos estão . Agora, vamos encontrar as extremidades. Para , temos
Para , temos
Beleza, agora podemos desenhar a elipse
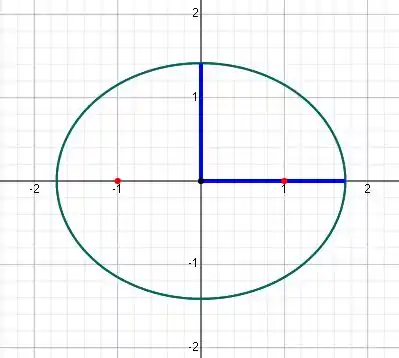
Passo 3
Então, os focos são . Vamos calcular as extremidades. Para , temos
Para , temos
O desenho da elipse fica assim
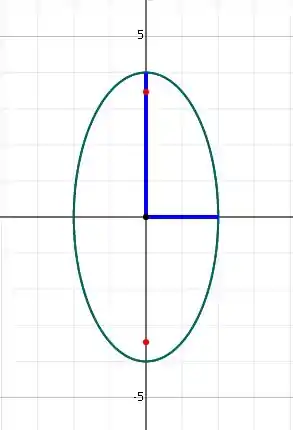
Resposta
Veja as figuras acima