Esboce, no mesmo plano de coordenadas, os gráficos de para os valores dados de . (Utilize simetrias, translações verticais, translações horizontais, alongamento ou reflexão.)
Passo 1
Olááá, tudo bem?
Nesta questão vamos trabalhar com domínio e imagem de funções. O gráfico de uma função que contém apenas um termo que é depende de passa pela origem. Quando há mais termos ou uma constante multiplicando a variável , o gráfico sofrerá algumas mudanças sendo elas:
- Simetria
- Translação vertical
- Translação horizontal
- Alongamento ou compressão
- Reflexão
Pode ser de duas formas: se for par (gráfico é simétrico em relação ao eixo ) ou ímpar (gráfico é simétrico em relação a origem).
Ocorrerá quando aparecer uma soma de uma constante com a função . Se , haverá deslocamento do gráfico para cima de unidades. Se , haverá deslocamento do gráfico para baixo de unidades.
Ocorre quando aparece uma soma de uma constante no argumento da função . Se , haverá deslocamento do gráfico para a esquerda de unidades. Se , haverá deslocamento do gráfico para a direita de unidades.
Ocorre quando toda a função, ou apenas o argumento da função, é multiplicado por uma constante .
—Para o caso de multiplicar toda a função . Se , ocorrerá uma compressão do gráfico da função, ficando menor (mais achatado) na direção vertical. Se , ocorrerá um alongamento do gráfico da função, ficando maior (mais alongado) na direção vertical.
— Para o caso de multiplicar apenas o argumento . Se , ocorrerá um alongamento do gráfico da função, ficando maior (mais alongado) na direção horizontal. Se , ocorrerá uma compressão do gráfico da função, ficando menor (mais achatado) na direção horizontal.
Ocorre quando os gráficos são refletidos entorno de um eixo de reflexão.
— Quando se quer refletir o gráfico em relação eixo , ou seja, a função refletida estará do outro lado do eixo , o gráfico se torna .
— Quando se quer refletir o gráfico em relação eixo , ou seja, a função refletida estará do outro lado do eixo , o gráfico se torna .
Passo 2
Compreendendo os conceitos do Passo 1, vamos começar a resolução.
O enunciado nos deu a função abaixo com variação da constante para os valores .
Observe que a variável está dentro do radicando o que nos diz que o gráfico apresenta apenas valores positivos. Há uma constante multiplicando a variável , haverá o alongamento vertical. A constante está em subtração com o argumento o que indica um deslocamento horizontal, para esquerda ou para direita, a depender do sinal de .
- Para , o gráfico permanecerá com o centro na origem,
- Para , o gráfico irá se deslocar para cima com ponto mínimo no ponto ,
- Para , o gráfico irá se deslocar para baixo com ponto mínimo no ponto ,
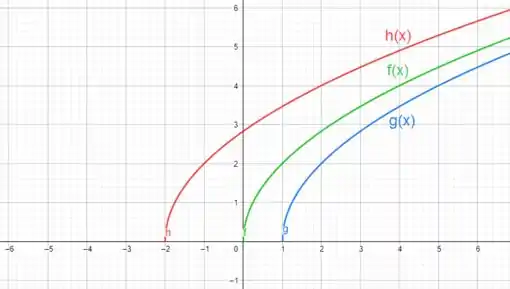
A seguir temos o gráfico com as três funções.
Até a próxima!! =]