Esboce a região delimitada pelos gráficos das equações e calcule a área.
Passo 1
Olááá, tudo bem??
Nessa questão vamos trabalhar com integração definida e antes de pôr as contas na ponta do lápis, vamos fazer uma rápida revisão sobre esses conceitos.
Se e são funções contínuas e para todo em , então a área da região delimitada pelos gráficos de , , e é
A fronteira superior é a função da curva de cima e a fronteira inferior é a função da curva debaixo. Esta fórmula também é válida para números negativos.
Algumas funções simples já tem suas antiderivadas tabeladas, o que facilita o cálculo de funções que são a mistura de algumas delas ou de funções mais complexas. A seguir, temos algumas propriedades:
Passo 2
O nosso primeiro objetivo é esboçar os gráficos das equações dadas e identificar a área delimitada por eles. Para esboçar um gráfico temos que adotar valores de arbitrários de para encontrar vários pontos e traçar a curva. Abaixo temos o gráfico com a área entre eles destacada.
- Azul
- Verde
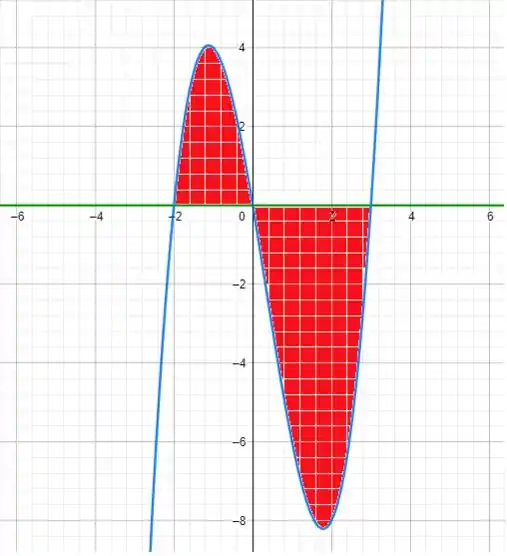
Passo 3
Para o cálculo da área, temos que identificar as funções que representam as fronteiras superior e a inferior e os pontos do intervalo . Observe que o gráfico apresente 2 áreas separadas pelo eixo . Devido ao fato de que elas são bem definidas e não simétricas, temos que calcular as duas áreas. Assim, considerando a área do lado esquerdo do eixo Y
- Fronteira superior
- Fronteira inferior
- Ponto
- Ponto
Para a área do lado direito do eixo Y
- Fronteira superior
- Fronteira inferior
- Ponto
- Ponto
Agora vamos substituí-los na fórmula da área e resolver a integral
Logo,
Até a próxima! =]