Escreva uma equação do plano definido pelo ponto e a interseção do plano com o plano .
Passo 1
Vamos chamar o ponto de ponto P
Vamos começar encontrando a interseção do plano com o plano .
O plano é aquele cuja equação é .
Então, temos que substituir :
É a equação de uma reta.
Passo 2
Vetor normal é aquele que é perpendicular ao plano, geralmente é descrito por .
Mas, temos uma equação geral do plano que é obtida com o vetor normal e um ponto do plano: .
Esse vetor normal pode ser obtido pelo produto vetorial entre o vetor diretor da reta e o vetor gerado pelo ponto de origem do vetor diretor da reta e um ponto do plano.
Vamos descobrir o vetor diretor da reta:
Para isso, vamos determinar um vetor pertencente a essa reta, lembrando que z=0:
Supondo temos que , ou seja, o ponto pertence à reta.
Supondo temos que , ou seja, o ponto pertence à reta.
Assim, temos que o vetor diretor da reta será .
O vetor gerado pelo ponto de origem do vetor diretor da reta e o ponto do plano será .
Passo 3
Agora é só calcular o produto vetorial :
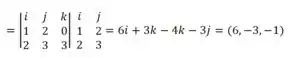
e , então:
.