- Escreva equações paramétricas da reta que passa pelos pontos e .
- Verifique se os pontos , e pertencem à reta .
- Localize na reta os pontos que a ela pertencem , inclusives os pontos e .
Passo 1
- Pessoal, a reta que passa pelos pontos e tem vetor diretor igual a :
- Temos que verifique se os pontos , e pertencem à reta . Para fazer isso, a gente tem que substituir cada ponto na equação paramétrica da reta e verificar se existe um único valor de que garanta as três igualdades. Temos
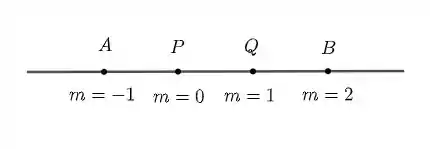
- Como a reta começa em , esse é o ponto em que . Já para , obtemos o ponto . O ponto corresponde a e o ponto a . Temos, da esquerda para a direita, do menor valor de até o maior valor de :
Vamos considerar que a reta começa em . Assim, as equações paramétricas da reta são
Passo 2
Ponto :
Como encontramos o mesmo valor de , então o ponto pertence a reta.
Ponto :
O ponto também pertence à reta.
Ponto :
Opa! temos dois valores diferente de . Logo, o ponto não pertence à reta.
Passo 3
Resposta
- pertencem a reta, não pertence.