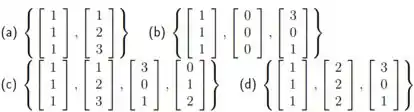
Fazendo o mínimo necessário de contas, diga se são bases de :
Passo 1
Salve, aluno do Responde Aí! Topa destruir essa questão?
Olha só, o primeiro passo para sabermos se uma matriz é base de é provar que ela é Linearmente Independente (LI), começamos arrumando os termos da seguinte forma:
- Organizamos os termos em forma de matriz e escalonamos:
- Faremos o mesmo processo da letra A, então, vamos organizar a matriz e escalonar:
- Faremos o mesmo processo da letra A, então, vamos organizar a matriz e escalonar:
- Faremos o mesmo processo da letra A, então, vamos organizar a matriz e escalonar:
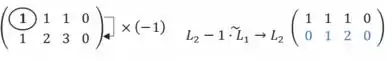
Uma forma bem fácil de resolver a partir daqui é relembrar do Teorema de Rouché-Frobenius sobre Posto, a ideia é o seguinte, pega a matriz e comparar com a matriz escalonada obtida, respectivamente:
![]()
Confere que a classificação do posto da matriz é igual ao número de linhas não-nulas. Nesse caso, a matriz inicial tem posto=2 e a escolanada também, porém não é igual ao número de incógnitas (x,y,x). Ou seja, o sistema é compatível e indeterminado (existem infinitas soluções), com mais de uma solução e, portanto, não é linearmente independente e nem base!
Passo 2
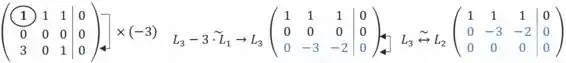
Comparando o posto, a matriz inicial tem posto=2 e a matriz escalonada também tem posto=2, porém não é igual ao número de incógnitas (x,y,x). Ou seja, o sistema é compatível e indeterminado (existem infinitas soluções), com mais de uma solução e, portanto, não é linearmente independente e nem base!
Passo 3

Se você prestar atenção, a matriz escalonada gera um sistema de fácil resolução, olha só:
ou seja
Sendo , então a solução é ÚNICA e portanto Linearmente Independente e base de .
Passo 4
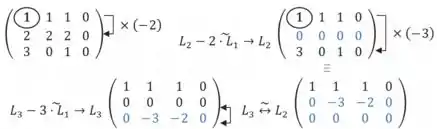
Sabendo que a matriz escalonada também tem posto=2, porém não é igual ao número de incógnitas (x,y,x). Ou seja, o sistema é compatível e indeterminado (existem infinitas soluções), com mais de uma solução e, portanto, não é linearmente independente e nem base!
Resposta
- Não é base ; b)Não é base ; c) é Base ; d) Não é base