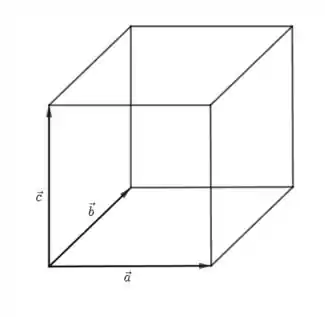
A figura a seguir é um cubo. Sejam , e
- Os vetores , e são l.i. ou l.d.? Justifique sua resposta.
- Demonstre que é base.
- Determine as coordenadas de na base .
Passo 1
- Fala, galerinha! Para determinar se , e são l.i. ou l.d., só precisamos verificar se o determinante da matriz que contém os três vetores é nulo ou não. Antes de fazer isso, vamos escrever esses vetores na base . A questão não fala explicitamente que essa é uma base, mas temos três vetores que são l.i. (todos são ortogonais entre si), então eles formam uma base. Assim, temos
- Seguindo um raciocínio parecido com o do item anterior, só precisamos calcular o determinante de uma matriz contendo os vetores e verificar se eles são l.i., ou seja, se o determinante é diferente de zero. Vamos usar os vetores obtidos no item a) e . Vamos lá!
- Para determinar as coordenadas de na base , só precisamos escrever esse vetor como combinação linear de
Agora podemos calcular o determinante:
Como o determinante é nulo, então esses vetores são l.d.
Passo 2
Com isso, vemos que os vetores são l.i. e é uma base.
Passo 3
Comparando os dois lados da equação, vemos que
Substituindo a terceira equação na segunda, obtemos
Agora, substituindo na primeira equação, obtemos
Depois de substituir todos os valores , e em , obtemos
Resposta
- São l.d.
- Olhar resolução