Em geral, a multiplicação de matrizes não é comutativa (isto é, AB BA). No entanto, existem certos casos especiais em que a comutatividade é válida. Mostre que:
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- Seja A e B duas matrizes diagonais . Então nós temos que e se
- Seja A uma matriz e deixamos onde são escalares
Definindo e nós temos que e
Vamos analisar os produtos e
Se nós temos que e para todo por causa:
Quando e nós temos que
Quando desde nós temos que
Quando , desde nós temos que e
Daqui se nós temos que e
Assim, temos que C e D são diagonais.
Se nós temos que e Daqui e
Assim temos que e então isso é
Observe que os elementos diagonais de AB são os produtos dos elementos diagonais correspondentes de A e B.
Passo 2
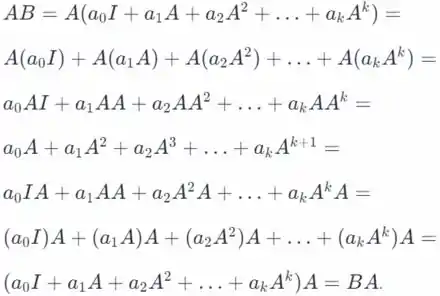
Resposta
Resposta nos passos.