Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo Exercícios Adicionais.1 - Ex. 25

A B C D E F é um hexágono regular de centro O . P é um ponto de segmento O B tal que O P → = 1 4 O B → . N é a interseção de A B ̄ e D P ̄ . Sendo: O A → = a → , O B → = b →   e A N → = α A B → , determine α .

Passo 1

Ok, galera. Vamos começar usando as informações de P é um ponto de segmento O B tal que O P → = 1 4 O B → . N é a interseção de A B ̄ e D P ̄ para tentar desenhar o hexágono:

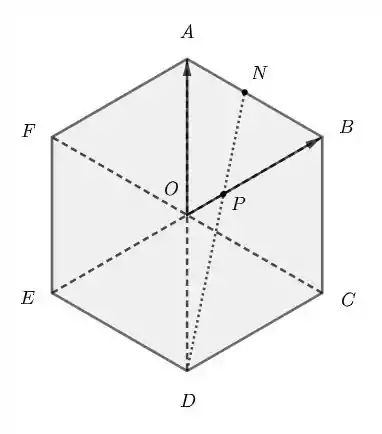
Melhor assim né? Com o desenho fica bem mais simples. Agora, vamos usar O A → = a → , O B → = b →   e A N → = α A B →

A N → = α A B → = α ( A O → + O B → ) = α ( - O A → + O B → ) = α ( - a → + b → )

Por outro lado, temos

A N → = A D → + D N →

É fácil identificar que A D → = - 2 a → mas D N → é um pouco mais complicado. Temos que notar que

D N → = β D P → = β ( D O → + O P → ) = β ( O A → + 1 4 O B → )

Então,

A N → = A D → + D N → = - 2 a → + β ( O A → + 1 4 O B → ) = - 2 a → + β ( a → + 1 4 b → )

Passo 2

No passo anterior, nós conseguimos duas expressões para A N → que, obviamente, devem ser iguais. Então,

A N → = α ( - a → + b → ) = - 2 a → + β ( a → + 1 4 b → )

⇒ ( 2 - α - β ) a → = ( 1 4 β - α ) b →

Como a → , b → não são paralelos, a equação acima só é verdadeira se tivermos um vetor nulo em ambos os lados. Nesse caso, temos que ter

1 4 β - α = 0 ⇒ α = 1 4 β

2 - α - β = 0 ⇒ 2 - 1 4 β - β = 0

⇒ 5 4 β = 2 ⇒ β = 8 5

Substituindo β = 8 5 em α , obtemos

⇒ α = 1 4 β = 1 4 8 5 = 2 5

Resposta

α = 2 5