No hexágono regular , e são pontos médios dos lados onde se situam. Escreva em função de .
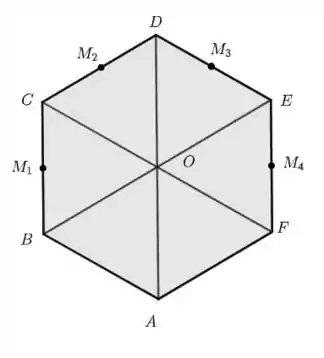
Passo 1
Tudo beleza, pessoal? Vamos começar essa questão escrevendo cada vetor :
Agora vem o pulo do gato. Veja bem, temos um triângulo e é ponto médio de . Então, podemos usar o resultado do Exercício Resolvido 3 do Capítulo 1:
Vamos seguir o mesmo raciocínio para os demais pontos:
Passo 2
Usando os resultados do passo anterior, ficamos com
Agora, só resta notar que
Então
onde usamos a soma de vetores na penúltima igualdade. Então, juntando tudo isso, ficamos com