Um holofote é projetado de modo que toda secção transversa contendo seu eixo de simetriz seja uma parábola com a fonte de luz no foco. Onde está o foco se o refletor tem de abertura e de profundidade.
Passo 1
Eaew, tudo bem?
A questão de hoje requer um pouquinho de visualização, imagine que a seção transversa que passa exatamente sobre o eixo de simetria deste holofote é uma parábola, tal como a seguinte:
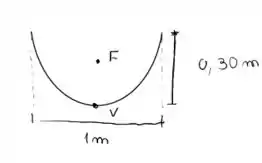
Podemos estabelecer um sistema de coordenadas sobre esta seção transversal e assim encontrar quais são as coordenadas do foco, belezinha?
Passo 2
Vamos colocar a origem sobre o vértice desta parábola, ou seja, seguindo a equação da parábola tal que:
Temos que e , são nulos, uma vez que estabelecemos o vértice na origem, sendo assim, temos:
Temos que o foco está posicionado à uma distância do vértice, portanto, precisamos do valor de para encontrar sua posição, vamos fazer isso no próximo passo!
Passo 3
Com nossa escolha da origem sobre o vértice, temos que um ponto que pertence a nossa parábola é dado pela extremidade do holofote como . Com este ponto em mãos podemos utilizar a equação 1 para encontrar o valor de , saca só!
Ou seja, o foco está à uma distância de do vértice de nossa parábola. Essa questão é isso, até a próxima, tchau tchau!