Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 6.3 - Ex. 10
Identificar a cônica, achar a equação no último sistema de coordenadas utilizado e fazer um esboço do gráfico.
Passo 1
Nossa equação é , podemos escrever essa equação na seguinte forma
onde a matriz carrega as informações a respeito dos valores quadráticos em x e y e a matriz a respeito dos valores lineares. Podemos ainda escrever o termo quadrático como , daí a matriz ganha o seguinte formato
repare ainda que os coeficientes de e estão nas diagonais (1 e -1) e os coeficientes dos termos cruzados nos outros termos. Quanto a matriz, temos
O nosso objetivo é realizar uma transformação de coordenadas de forma que a cônica em questão esteja centralizada no novo sistema de coordenadas. Esse novo sistema de coordenadas está ligado com a matriz diagonalizada da matriz e com seus autovetores.
Passo 2
Para diagonalizar a matriz , começamos com o polinômio característico , que é dado por
e suas raízes são . Segue que, a matriz diagonalizada é
e encontrando seus autovetores, através da equação
onde é a matriz identidade , encontramos os seguintes autovetores (já normalizados)
para e para
Passo 3
Tendo os autovetores e autovalores em mãos, escrevemos a equação da cônica como
onde representa o novo sistema de coordenadas e é a matriz ligada aos autovetores que nós encontramos
daí, nossa equação no novo sistema de coordenadas se torna
completando o quadrado em ambas as variáveis
rearranjando a equação
Passo 4
Por fim, vamos realizar mais uma transformação de sistema de coordenadas
e obtemos então, a equação da seguinte cônica:
que é uma hipérbole e seu gráfico é dado por
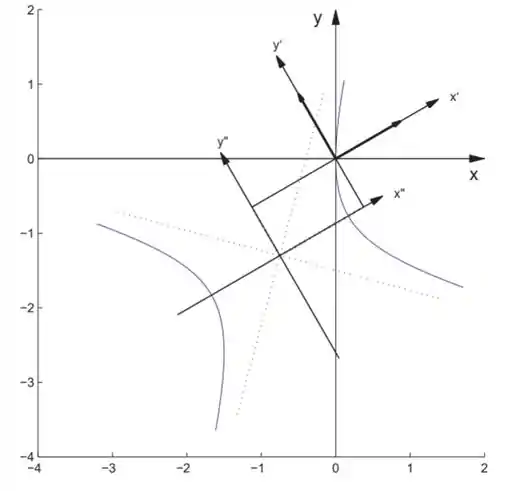
a primeira transformação de coordenadas, nos levou a um sistema de coordenadas onde os eixos são os autovetores que encontramos no início do problema. A segunda apenas trouxe a origem do sistema para o centro da cônica (é por isso que os vetores dos eixos x’ e x’’ são paralelos, apenas fizemos uma translação).
Resposta
Ei, a resposta está no passo a passo :)