A interseção das superfícies esféricas e é uma circunferência.
- Determine uma equação do plano que contém a circunferência e,
- determina o centro e o raio da circunferência.
Passo 1
Fala, pessoal! Se você está com dificuldade nessa questão, vem comigo que vai dar bom. Antes de começar a resolver, vamos escrever as equações das duas esferas na forma reduzida:
Primeira esfera:
O centro da primeira esfera é em e o raio é .
Segunda esfera:
O centro da segunda esfera é em e o raio é . Agora, podemos começar a resolver a questão.
Passo 2
- Para determinar o plano, precisamos do seu vetor normal. Mas, esse vetor normal está na mesma direção que o vetor
- Para calcular o centro da circunferência e seu raio. A figura abaixo ilustra mais ou menos o que está acontecendo
Então, o plano terá a forma
Só falta a gente encontrar . Para isso, temos que usar um ponto que pertença ao plano e substituí-lo na equação do plano para resolver para . Esse ponto é justamente o centro da circunferência, que vamos calcular no próximo item. Então, vamos resolver o próximo item e depois voltar nesse.
Passo 3
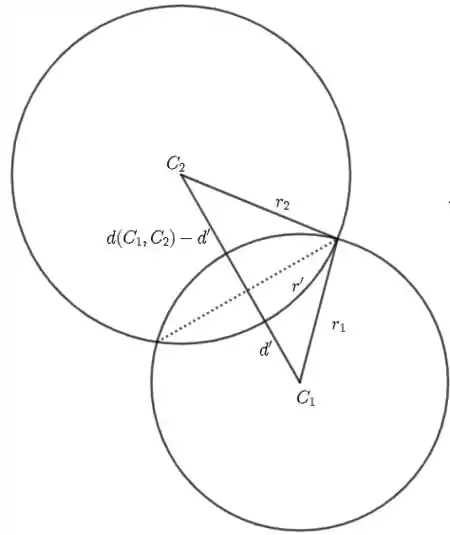
É possível notar que a distância de interseção será dada por:
Agora, vamos subtrair uma equação da outra
Nessa equação, a única coisa que falta é descobrir a distância entre os dois centros. Para isso, calculamos o módulo do vetor :
Então,
A partir dessa distância, podemos obter o raio da circunferência a partir da seguinte equação:
Lembrando que , temos um vetor que sai de até , que tem o mesmo sentido de , ou seja, e cujo módulo vai ser igual a distância entre e :
Então, . Como , então
.
Passo 3
Agora, vamos voltar rapidinho no item a), onde conseguimos o plano
e substituir o ponto nessa equação:
Assim,
Resposta
- e