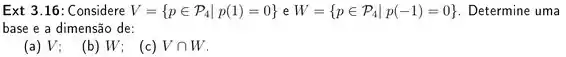
Passo 1
Oi oi, aluno Responde aí, vamos resolver essa questão facinha?
- A primeira coisa a fazer é escrever os elemento em na forma:
- A letra b) segue a mesma ideia de reescrever os elemento em na forma:
- A letra c) também segue a mesma ideia, mas devem ser consideradas as duas restrições das letras a) e b), logo:
Aí basta aplicarmos a condição p(1)=0
A equação p(1)=0 depende de quatro variáveis x acompanhadas das letras “a”, “b”, “c” e “d”, logo, possui 4 dimensões.
E a base pode ser escrita no modelo
Passo 2
Aí basta aplicarmos a condição p(-1)=0
A equação p(-1)=0 depende de quatro variáveis x acompanhadas das letras “a”, “b”, “c” e “d”, logo, possui 4 dimensões.
E a base pode ser escrita no modelo
Passo 3
Ou seja, se b+d=0, a dimensão é 3, assim, se apenas “c”, “d” e “e” forem usados como parâmetros, a base é escrita como: