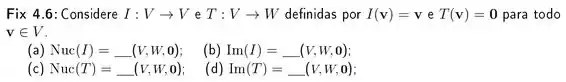
Passo 1
- Para encontrarmo o núcleo de uma transformação linear , denotado por Nuc (I), é um conjunto dos vetores do domínio cuja imagem é o vetor nulo, por exemplo
- Para encontrarmos a imagem de uma transformação linear usamos a definição de que , denotada por Im(I), é o conjunto dos vetores do contradomínio que são imagem de algum vetor do domínio, logo temos:
- Para encontrarmo o núcleo de uma transformação linear , denotado por Nuc (T), é um conjunto dos vetores do domínio cuja imagem é o vetor nulo, por exemplo
- Para encontrarmos a imagem de uma transformação linear sendo , denotada por Im(T), é o conjunto dos vetores do contradomínio que são imagem de algum vetor do domínio, logo temos:
Ou seja, para que o vetor seja zerado, necessariamente temos que ter
Passo 2
Assim, se , consideramos que Im(I) = V
Passo 3
Ou seja, para que o vetor seja zerado, basta v assumir qualquer valor, sabendo que , diremos que
Passo 4
Assim Im(T) = 0
Resposta
; ;