![]()
Passo 1
Essa questão é molezinha, pois aborda conteúdo basicão de multiplicação de matrizes. A ideia é provar que o produto de matrizes é:
- Associativo? Ou seja, se estamos multiplicando três ou mais números, é possível associar os fatores de maneiras diferentes e mais convenientes. Portanto:
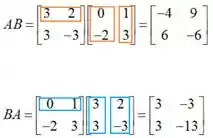
- Comutativo? Nãaaao, aqui basta lembrar da propriedade mais fácil da multiplicação de matrizes de que ela não segue a regra da multiplicação de escalares, ou seja, para número escalares tanto faz a ordem, pois 5*7=7*5=35, mas para matrizes A*B ≠ B*A, assim como o exemplo abaixo
- Distributivo? Esta propriedade diz que “a multiplicação da soma é a soma das multiplicações” , portanto, Se S, T e U forem matrizes geradas de transformações lineares, podemos escrevê-los como:
Se S e T forem matrizes geradas de transformações lineares e k for escalar, temos
Passo 2
Passo 3
Resposta
- Associatividade ; c) distributividade