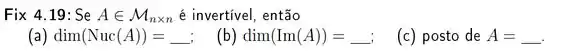
Passo 1
Mais uma questão de pura teoria, mas é mais simples do que parece, olha só.
- Como descobrir a dimensão do núcleo de A, sendo que ? A primeira coisa é perceber que o comando diz que a A é invertível, ou seja, possui função inversa, se, e somente se, ela for bijetora que é uma função injetora, ou seja, todo elemento da imagem possui um único correspondente no domínio. Até aqui, tudo beleza, né? O importante nesse passo é lembrar do teorema que diz que A para ser invertível tem que satisfazer a condição de ter e, consequentemente, a dimensão
- E a dimensão ? Bom, nós já sabemos que a função é inversível, ou seja, , a dimensão do espaço-linha é o número k de linhas não-nulas após escalonar A. Como o sistema possui n variáveis e foi reduzido a k equações, concluímos que são n − k variáveis livres, isto é, o Nuc(A) possui dimensão n – k, portanto:
- Posto da matriz A (a dimensão de sua imagem) é igual ao número de linhas não-nulas da matriz escalonada, como sabemos que a matriz A tem n linhas e 0 são nulas, o posto de A é .
Passo 2
DE acordo com a letra a), , logo:
Passo 3
Resposta
- ;
- ;
- .