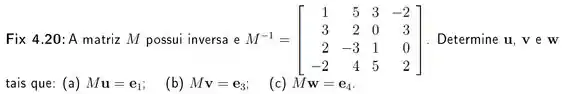
Passo 1
Partiu mais uma questão? Se liga que essa aqui tá tentando te enganar parecendo difícil, mas na verdade é moleza moleza!
Para resolvermos essa questão teremos que lembrar da propriedade que diz que se temos uma função invertível, ou seja, se a multiplicação de matrizes gera uma matriz identidade, . Temos que se escalonarmos a matriz A, da seguinte forma
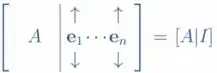
obtendo a matriz identidade à esquerda e a solução dos sistema no lado direito. Essa propriedade nos permite associar que a inversa de A é igual à matriz B, assim como representado abaixo.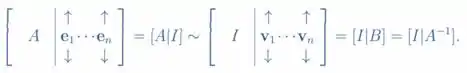
Passo 2
Até aqui tá beleza! Agora só basta aplicar essa propriedade à questão, se a matriz M de fato é invertível, ou seja, a multiplicação de matrizes gera uma matriz identidade, , sendo x uma matriz desconhecida, temos que a inversa de M é a própria matriz x, da seguinte forma:
Se
- A letra a) pede , a linha de x, portanto:
- A letra b) pede , a linha de x, portanto:
- A letra c) pede , a linha de x, portanto: