![]()
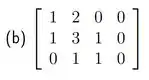
Passo 1
Partiu mais uma questão!
Se liga que o primeiro passo para obter a base é escalonar a matriz
Depois disso basta escrever as variáveis em um sistema:
,
.
Resolvendo temos que o núcleo é com dimensão .
Passo 2
O segundo passo é obter a imagem, para isso faremos o mesmo processo de escalonamento com a matriz transposta, desse modo:
Portanto, a imagem é e tem dimensão
Resposta
b)