Mostre que um espelho hiperbólico, reflete na direção de um foco, os raios que incidem na hipérbole na direção do outro foco, seguindo os seguintes passos:
c) Mostre que . Logo o triângulo é isósceles e assim o ângulo de reflexão do raio que passa por depois de ser refletido em e o ângulo de incidência do raio que se reflete em vindo de , são iguais. Portanto, o raio que vem de e se reflete em necessariamente passa por
Passo 1
Fala aiii meus lindos tudo blz? espero que sim
Então se liga só nessa questão do livro de álgebra linear do Reginaldo Santos ele pede para mostrar que um espelho hiperbólico, reflete na direção de um foco, os raios que incidem na hipérbole na direção do outro foco, seguindo os seguintes passos:
c) Mostre que . Logo o triângulo é isósceles e assim o ângulo de reflexão do raio que passa por depois de ser refletido em e o ângulo de incidência do raio que se reflete em vindo de , são iguais. Portanto, o raio que vem de e se reflete em necessariamente passa por

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Dada a representação gráfica,
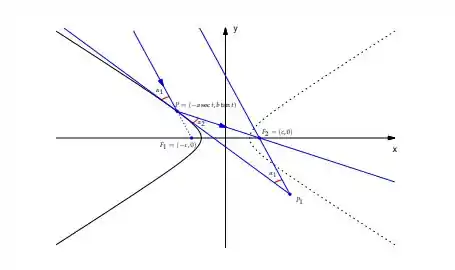
Vamos ter que,
Ficando o seu raio definido por,
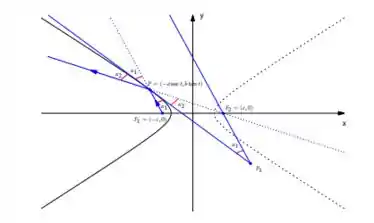
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
Imagem ilustrada no passo anterior.