Mostre que o gráfico é a reflexão do gráfico de em relação à reta , verificando as condições seguintes
- Se está no gráfico de , então está no gráfico de .
- O ponto médio do segmento está na reta .
- A reta é perpendicular à reta .
Passo 1
Olááá, tudo bem??
Nessa questão vamos trabalhar com funções inversas e antes de por as contas na ponta do lápis, vamos fazer uma rápida revisão do que é essa tal “função inversa”.
Para que uma função admita uma inversa, ela precisa ser bijetora, ou seja, deve ser ao mesmo tempo injetora (todo elemento da imagem possui um único correspondente no domínio) e sobrejetora (não há nenhum elemento da imagem que não tenha um elemento do domínio associado a ele). A imagem abaixo ilustra o que acabamos ler
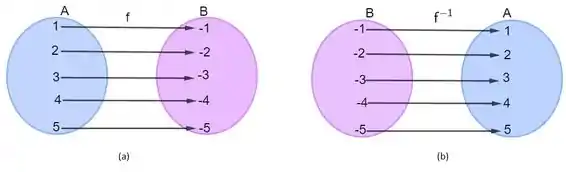
Definindo formalmente, seja uma função bijetora com domínio e contradomínio . Se é uma função com domínio e contradomínio , então é inversa de se e somente se as seguintes condições forem válidas:
Passo 2
Compreendendo a definição de função inversa, vamos resolver a questão.
Para verificar as condições, vamos adotar uma função arbitrária, . O gráfico está plotado abaixo
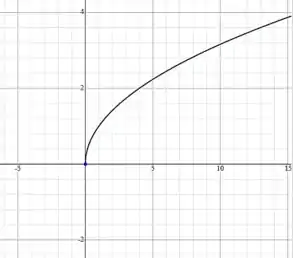
Passo 3
Próximo passo é encontrar a inversa da função
Invertendo as variáveis
Isolando a variável
Vamos impor a restrição de para que a função seja bijetora. Portanto, o gráfico de é
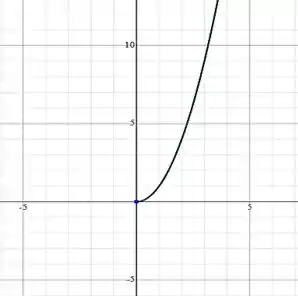
Passo 4
Agora que já obtemos as duas funções e seus respectivos gráficos, vamos adotar um ponto aleatório para teste. Para e . As curvas e os pontos estão plotados na figura abaixo
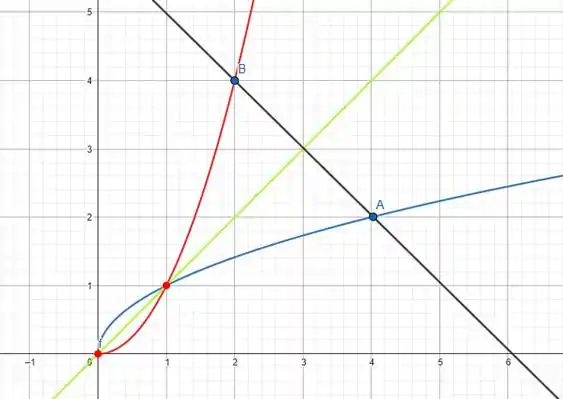
- A linha azul é a função .
- A linha vermelha é a função .
- A linha verde é a função .
- A linha preta é a reta que une os pontos e
O gráfico plotado por si só satisfaz as condições (ii) e (iii) e com isso resolvemos a questão
Até a próxima =]
Resposta
Ei, a resposta está no passo a passo :)