Mostre que qualquer que seja o valor de , o módulo do vetor é igual à área do paralelogramo definido pelos vetores
Passo 1
Vamos primeiro encontrar o valor do módulo do vetor :
O módulo do vetor é dado por
Então, para , temos:
Passo 2
Agora vamos determinar a área do paralelogramo definido pelos vetores
Temos a fórmula para calcular a área de um paralelogramo definido por dois vetores :
Então, teremos que calcular o produto vetorial :
O produto vetorial de é dado por :
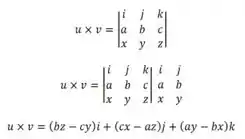
Substituindo por , temos:
Passo 3
Agora é só calcular o módulo do produto vetorial!
Mas, isso é exatamente o módulo
Então, .
Resposta
Ei, a resposta está no passo a passo :)