é um paralelogramo. e . O ponto é tal que e é tal que .
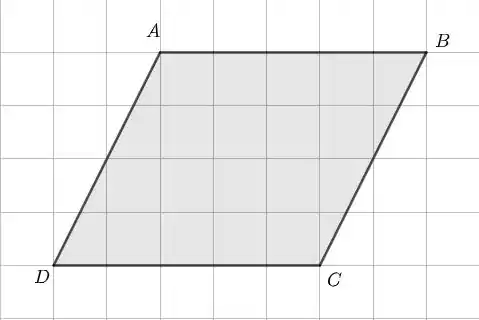
- Desenhe o paralelogramo e marque os pontos e na figura.
- Escreva em função de e .
- Se e , escreva em função de e .
Passo 1
- Galera, antes de mais nada, temos que lembrar que num paralelogramo os lados opostos são paralelos e de mesmo comprimento. Esse detalhe vai ser importante durante a resolução. As dimensões e ângulos internos não importam muito contando que essas propriedades sejam satisfeitas. Então, você pode desenhar o seu paralelogramo preferido sem problemas:
- Agora, vamos escrever em função de e :
- Nesse item, temos que escrever em função de e :
Para marcar e na figura, temos que usar e para calcular
Com isso, concluímos que está a dois quintos do segmento ligando a e está a metade do segmento ligando a . Assim, podemos marcar esses pontos no paralelogramo:
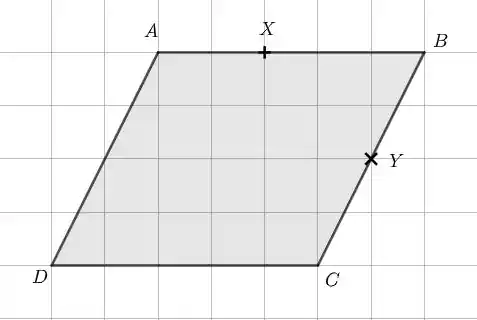
Passo 2
Ufa! Essas contas foram um pouquinho longas, mas finalmente chegamos ao resultado. Na primeira linha, nós fizemos algumas decomposições para tentar obter os vetores que já conhecemos. Na segunda linha, substituímos os resultados do Passo 1, organizamos os vetores e, por fim, utilizamos a propriedade do paralelogramo de que lados opostos são paralelos e de mesmo comprimento . Na terceira linha, substituímos e .
Passo 3
Na primeira linha, fizemos a soma de vetores e utilizamos os resultados e . Na segunda linha, utilizamos a propriedade do paralelogramo . Assim, ficamos com
Resposta
b)
c)