Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo Exercícios Adicionais.1 - Ex. 22

A B C D é um paralelogramo. E é tal que A D →   = 5 D E → e F é tal que 4 A F →   =   5 A B → . G é a interseção de A C ̄ e E F ̄ . Sendo A G → = m A C → , determine m .

Passo 1

A equação A D →   = 5 D E → indica que o ponto E está fora do paralelograma e que A D → tem cinco vezes o tamanho de D E → . A equação 4 A F →   =   5 A B → também indica que F está fora do paralelogramo pois, nesse caso, temos A F →   =   5 4 A B → .

O paralelogramo dessa questão fica mais ou menos assim:

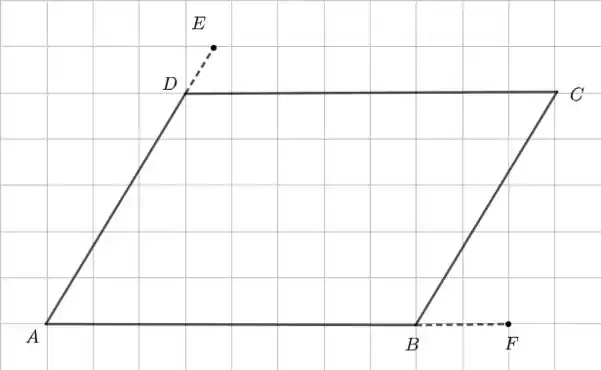
Agora, vamos acrescentar o ponto G que é a interseção de A C ̄ e E F ̄ :

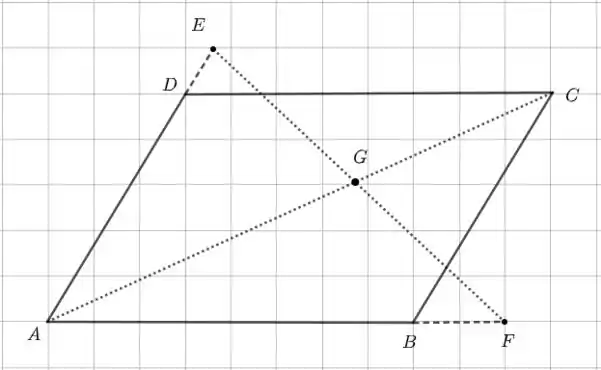
Passo 2

Temos A G → = m A C → , mas também podemos escrever

A G → = A E → + E G →

Mas, temos que notar que E G → = n E F → e

A E → = A D → + D E → = A D → + 1 5 A D → = 6 5 A D →

E F → = E A → + A F → = - A E → + A F → = - 6 5 A D → + 5 4 A B →

A C → = A D → + D C → = A D → + A B →

Então, podemos escrever tanto A G → = m A C → = m ( A D → + A B → ) quanto

A G → = A E → + E G → = A E → + n E F → = 6 5 A D → + n ( - 6 5 A D → + 5 4 A B → )

Como as duas expressões devem ser iguais, então

m ( A D → + A B → ) = 6 5 A D → + n ( - 6 5 A D → + 5 4 A B → ) ⇒ ( m + 6 5 ( n - 1 ) ) A D → = ( 5 4 n - m ) A B →

⇒ ( m + 6 5 ( n - 1 ) ) A D → = ( 5 4 n - m ) A B →

A expressão acima indica que A D → , A B → são paralelos ou que os coeficientes multiplicando os dois vetores são nulos. Já sabemos que a primeira opção é falsa, então só nos resta

5 4 n - m = 0 ⇒ m = 5 4 n

m + 6 5 ( n - 1 ) = 0 ⇒ 5 4 n + 6 5 n - 6 5 = 0

⇒ 25 + 24 20 n = 6 5 ⇒ 49 20 n = 6 5

⇒ n = 6 5 20 49 = 4 ⋅ 5 ⋅ 6 5 ⋅ 49 = 24 49

Agora, substituímos n = 24 49 em m = 5 4 n :

m = 5 4 24 49 = 30 49

Resposta

m = 30 49