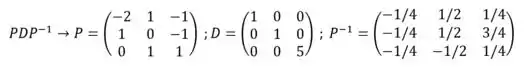Se possível, diagonalize a matriz:
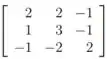
Passo 1
Saca só a resolução dessa questão! Para nós diagonalizarmos uma matriz, ela, primeiramente, deve ser diagonalizável, a condição é que encontremos os autovalores, assim:
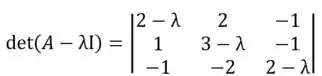
Desenvolvendo a equação, nós temos que , , . Portanto, por ter 3 autovalores em uma matriz 3x3 de dimensão 3, podemos dizer que a matriz é de fato diagonalizável !
Além disso, a matriz diagonal D é composta pelos autovalores, assim:
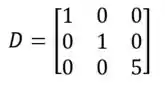
Passo 2
O próximo passo é diagonalizar a matriz, para isso, vamos substituir os autovalores da matriz para determinar os autovetores.
- Se
- Se vamos repetir o mesmo processo:
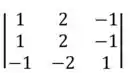
Fazendo eliminação de Gauss, temos:

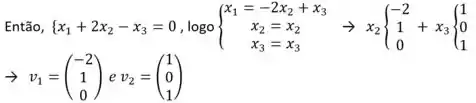
Passo 3

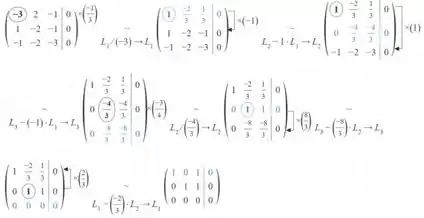
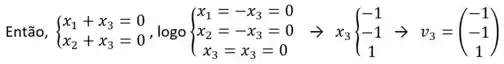
Portanto, os autovetores correspondente aos autovetores de D correspondem às colunas de P:
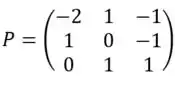
Passo 3
E por o último passo é inverter a matriz P, logo:
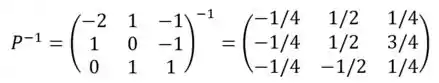
Resposta