Prove a associatividade para a multiplicação de matrizes 2 X 2, isto é, considere
e mostre que
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
-
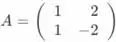
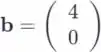
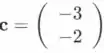
Os vetores de coluna de A
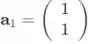
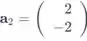
Para escrever b como uma combinação linear de e devemos encontrar números reais e de tal forma que o que nos dá que
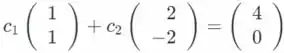
Então
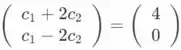
Por isso devemos ter e o que nos dá que e, em seguida, nos dando
Desde e temos que o que nos dá que e, em seguida,
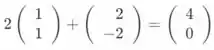
Passo 2
- De acordo com parte (a) deste exercício, temos que . Portanto, podemos concluir que é uma solução do sistema linear . Vamos determinar se existem ou não outras soluções computando a forma de escalonada de linha da matriz aumentada .
- Para escrever c como uma combinação linear das colunas e vamos calcular a forma de escalão de linha reduzida da matriz aumentada .
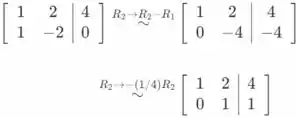
Da forma de escalonada de linha da matriz aumentada , podemos concluir que o sistema é consistente e tem uma solução única, porque não há variáveis livres. Portanto, é a única solução do sistema dado.
Passo 3
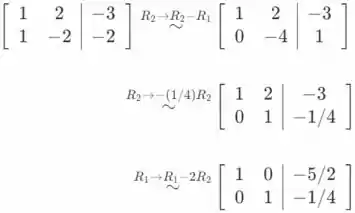
A partir da forma de escalão de linha reduzida, podemos concluir que
é a única solução do sistema linear (já que não há variáveis livres). Isso implica que a coluna c pode ser escrito como
Resposta
Resposta nos passos.