- Prove que a função linear definida por com , tem uma inversa, e determine .
- Uma função constante tem inversa? Explique
Passo 1
Olááá, tudo bem??
Nessa questão vamos trabalhar com funções inversas e antes de por as contas na ponta do lápis, vamos fazer uma rápida revisão do que é essa tal “função inversa”.
Para que uma função admita uma inversa, ela precisa ser bijetora, ou seja, deve ser ao mesmo tempo injetora (todo elemento da imagem possui um único correspondente no domínio) e sobrejetora (não há nenhum elemento da imagem que não tenha um elemento do domínio associado a ele). A imagem abaixo ilustra o que acabamos ler
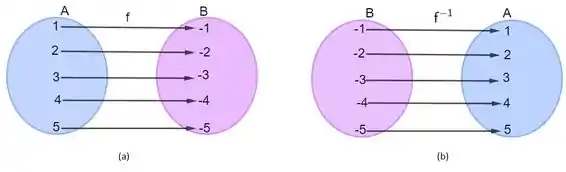
Definindo formalmente, seja uma função bijetora com domínio e contradomínio . Se é uma função com domínio e contradomínio , então é inversa de se e somente se as seguintes condições forem válidas:
Passo 2
Compreendendo a definição de função inversa, vamos resolver a questão.
- Há três passos que devemos seguir para resolvermos esta função:
— Primeiro: verificando se é uma função um-a-um (ou se é crescente e decrescente) em todo o seu domínio. Analisando a função dada, , concluímos que o gráfico da função é uma reta crescente () e intercepta o eixo no ponto .
— Segundo: Resolver a equação em relação a em termos de , obtendo uma equação da forma . Então,
Invertendo as variáveis,
Isolando a variável
Portanto
— Terceiro: verificar as duas condições (i) e (ii) citadas no Passo 1. Vamos começar pela (i) condição,
Onde houve vamos substituir pela expressão dentro da função inversa,
Eliminando os termos iguais, temos que
Agora para (ii) condição
Onde houve vamos substituir pela expressão dentro da função inversa,
Eliminando os termos iguais, temos que
Como todas as condições foram satisfeitas, provamos que com , tem uma inversa.
Mas calma, já estamos acabando. Falta só resolver mais um item.
Passo 3
(b) Função constante é toda função em que os elementos do domínio possuem uma mesma imagem. Com base no que foi explicado no Passo 1, uma função invertível é aquela em que todo elemento da imagem possui um único correspondente no domínio, o que não é verdade para a função constante, logo ela não possui uma função inversa.
Resposta
Ei, a resposta está no passo a passo :)