Qual é a relação de equivalência associada a cada uma das seguintes partições?
a)
b)
c)
Passo 1
Fala minha galera, bora fazer mais um exercício maravilhoso de algelin!
-
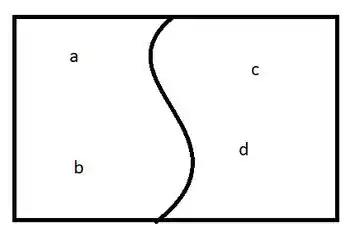 Como temos uma partição de conjuntos finitos, podemos desenhar, olha só
Como temos uma partição de conjuntos finitos, podemos desenhar, olha só -
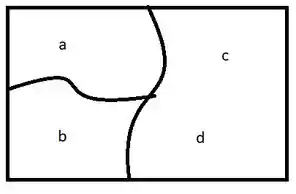 Vamos fazer o mesmo que fizemos para o item anterior.
Vamos fazer o mesmo que fizemos para o item anterior. - Como temos conjuntos infinitos não podemos continuar nosso incrível talento artístico, porque não dá pra desenhar infinito né. Porem, batendo o olho bem, percebemos que um conjunto representa os inteiros pares e o outro conjunto represente os inteiros impares, logo a união dos dois representa todos os inteiros!
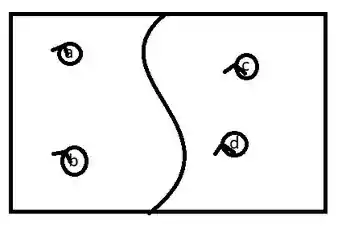 Primeiro vamos desenhar a relação reflexiva, ou seja, vamos fazer aquele laço que vimos a um tempinho atrás:
Primeiro vamos desenhar a relação reflexiva, ou seja, vamos fazer aquele laço que vimos a um tempinho atrás:
Agora vamos fazer a simétrica e transitiva, ligando com setas duplas os elementos do mesmo bloco, pois eles não se relacionam com o de outro bloco.
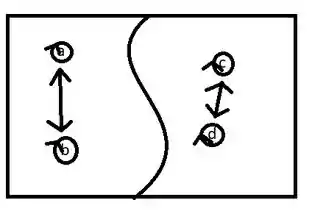 Finalmente podemos escrever todas as relações que encontramos:
Finalmente podemos escrever todas as relações que encontramos:
Simples, não? Vamos pra b!
Passo 2
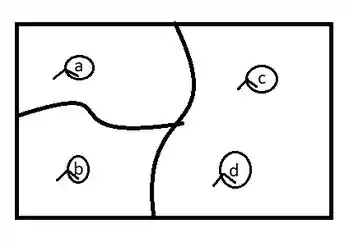 Agora desenhamos a reflexiva:
Agora desenhamos a reflexiva:
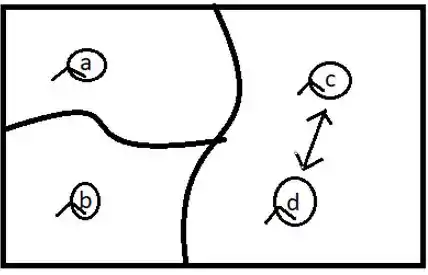 Próximo passo é ligar as setas duplas que pode existir:
Próximo passo é ligar as setas duplas que pode existir:
Por últimos, devemos escrever a relação gerada.
Bora terminar esse exercício!
Passo 3
Sabemos também da teoria que toda relação de congruência módulo m sobre os inteiros é uma relação de equivalência, por definição.
Como temos dois conjuntos, nossa relação de equivalência é dada por congruência módulo 2, isto é, escrevendo matematicamente:
Resposta
- .