Resolva a desigualdade e exprima a solução em termos de intervalos, quando possível.
Passo 1
Olááá, tudo bem??
Nessa questão vamos trabalhar com inequação e antes de pôr as contas na ponta do lápis, vamos fazer uma rápida revisão de suas propriedades.
Diferentemente de uma equação, a inequação do 1º grau expressa uma desigualdade na variável que pode ser reduzida em uma das formas
Em que e . Esses sinais servem para comparar. Para resolver uma inequação do 1º grau, deve-se determinar um conjunto com todos os valores para a variável de forma que a sentença se torne verdadeira.
Passo 2
Para resolvemos a inequação, vamos isolar a variável na sentença.
Passo 3
O próximo passo é encontrar o valor crítico que se encontra no denominador da divisão. Para que essa inequação exista, o denominador não deve ser igual a zero, logo para o primeiro caso,
Agora que encontramos o valor, vamos avaliar se ele deve ser maior ou menor que ele. Para que a igualdade da inequação permaneça, ou seja, fração da esquerda seja menor que a da direita, o denominador deve ser negativo, assim .
Para o segundo caso,
Para que a igualdade da inequação permaneça, ou seja, fração da direita seja maior que a da esquerda, o denominador deve ser positivo, assim .
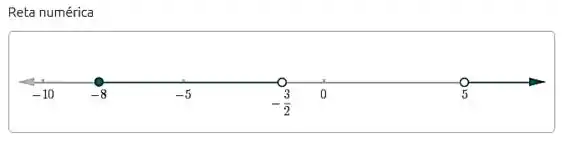
Passo 4
Logo, qualquer valor que esteja no intervalo satisfaz o problema.
Até a próxima! =]
Resposta