- Uma reta traçada pelo ponto é perpendicular ao plano . Desenhe a reta, escreva suas equações e determine as coordenadas dos pontos e da reta que distam unidades do ponto .
- Calcule a área do triângulo .
Passo 1
- Como a reta passa pelo ponto , esse vai ser o nosso ponto inicial. Vamos supor que o vetor diretor dessa reta seja da forma . Vetores perpendiculares ao plano são paralelos a (só a coordenada muda). Então, o vetor diretor da reta que queremos na verdade é da forma . Pronto, já podemos obter as equações parametrizadas da reta
- A área do triângulo é dada por
Assim, qualquer ponto desta reta será da forma . O vetor que liga a é
Agora, vamos usar a condição de que a distância desses pontos é . Isso quer dizer que o módulo do vetor é igual a :
Temos dois valores do parâmetro , um deles correspondendo ao ponto e o outro ao ponto :
Você pode conferir abaixo a figura com a reta e os pontos envolvidos:
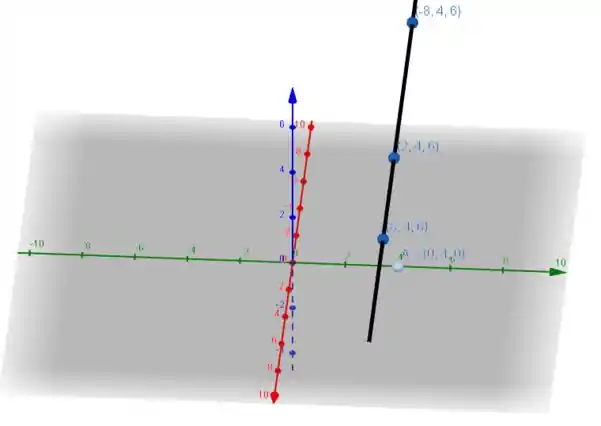
Passo 2
Primeiramente, vamos calcular esses vetores:
Assim, o produto vetorial será:
Finalmente, obtemos a área do triângulo:
Resposta
- ,