Sabe-se que três arestas adjacentes ao vértice de um paralelepípedo no são determinados pelos vértices , e . Calcule o volume do paralelepípedo.
Passo 1
Faaalaaa, galeraaaa!
Para resolver essa questão devemos calcular o volume do paralelepípedo através do determinante. Temos, então:
Pela regra de Sarrus, podemos repetir as duas primeiras colunas da matriz e a partir disso calcular seu determinante, como mostra o esquema abaixo:
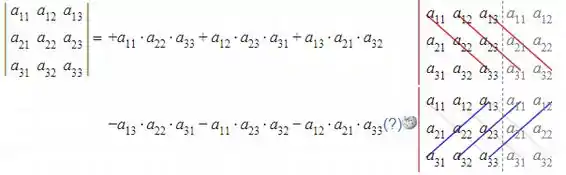
Passo 2
Para a matriz em questão temos, então:
Passo 3
O volume do paralelepípedo será:
Até a próxima!
