São dados os pontos , e .
- Determine um ponto tal que seja um paralelogramo com .
- Usando produto vetorial, calcule a área de .
- Determine um ponto na reta tal que seja perpendicular a .
- Calcule o produto . Se as respostas de e não “baterem”, descubra onde você errou.
Passo 1
- Ok! Vamos começar lembrando que e. Assim:
- O módulo produto vetorial nos dá a área do paralelogramo. Então, vamos calcular esses vetores
- Vamos determinar a forma genérica de um ponto na reta . Para isso, usamos como ponto inicial e como vetor diretor. Sendo assim, as equações paramétricas da reta serão
- Temos e
Passo 2
Agora, vamos calcular o produto vetorial:
Finalmente, podemos obter a área do paralelogramo:
Passo 3
Então, qualquer ponto na reta terá a forma . Agora, vamos calcular o vetor e obter o valor de para que ele seja perpendicular a . Temos
Agora, usando a condição de ortogonalidade:
Então, é o valor que satisfaz as condições que queremos. O último passo que falta é substituir esse valor no ponto :
Passo 4
Então, os módulos desses vetores são:
Assim, , como esperado. Para ficar mais fácil de entender o que aconteceu aqui, vamos relembrar que
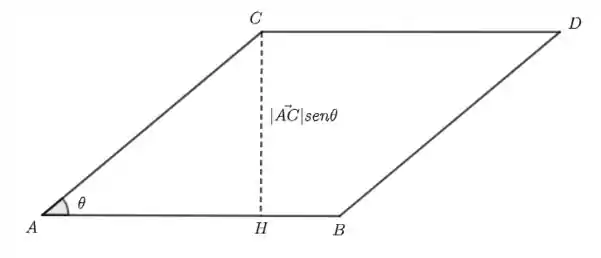
onde é o ângulo entre . Assim, é justamente a distância entre e a reta , que é numericamente igual ao módulo do vetor .